One to one functions
Summary:
For a function to be one to one, every \(x\) value has to give exactly one \(y\) value, and no \(y\) value can be given by more than one \(x\) value. Below is a depiction of a one to one function as a mapping of points:
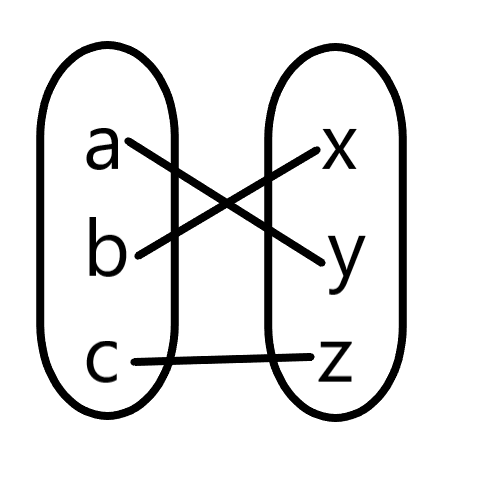
Example 1:
Determine which of the following is a one to one function:
First, lets eliminate choice a. We can do this by drawing any horizontal line above zero, since such a line would cross the graph in two places. This means that a fails the horizontal line test.
Next for b, we can elimnate it by drawing a vertical line with \(x\) greater than zero, which will also touch the line in multiple points causing it to fail the test.
c fails both tests, since it is a circle, so any vertical or horizontal lines (except for the ones exactly at the edges) within its domain or range will cause it to fail the tests
d passes both tests since no line, horizontal or vertical will touch it twice. Therefor the answer is d.
In the next example, we will do the same with functions given in the form of a table
Example 2:
Determine which of the following is a one to one function
Determining wether these are a function or not is even easier. All we have to do is look at both columns and look for repeated numbers. This means we can easily remove choice a as \(y=2\) is repeated. We can also remove choice c, since \(x=4\) is repeated. This means we get choice b, as our answer, and it is correct since no value is repeated in either column
Conlcusion:
In conclusion, you have learned how to identify One to one functions, a unique type of function in which each \(x\) value only corresponds to one \(y\) value and each \(y\) value only corresponds to one \(x\) value.
Next: Multiplying polynomials